Índices e impactos estudiosos

Definição

Às vezes chamado de bibliometria, os índices estudiosos são ferramentas matemáticas e estatísticas que medem a significância das contribuições feitas por um acadêmico ao seu campo de pesquisa. Os índices estudiosos podem incorporar outras avaliações, como rastreamento de citações e classificação de periódicos.

Criação

Qualquer agregador de citações e referências, pode, ter tempo, dinheiro e inclinação, gerar seu próprio conjunto de índices estudiosos. Os editores proeminentes neste campo incluem Elsevier e Thomson Reuters.

Software comercial que usa analisadores e mecanismos de pesquisa na Web para gerar conjuntos de índices estudiosos ou resultados individuais estão agora disponíveis. Os exemplos são: publicar ou perecer; 'ScholarIndex'; 'Scopus' e 'Google Scholar'.

Cada fornecedor de software usa principalmente seus próprios dados, bem como periódicos, publicações, arquivos de autoridade, índices e categorias de assuntos para produzir conjuntos de índices estudiosos.

Enquanto algumas empresas fornecem os dados e as métricas avaliadas como downloads gratuitos, outras exigem assinaturas para cobrir os custos de fabricação e manutenção de um analisador eficiente, mecanismo de pesquisa e banco de dados de documentos.

Usar

Os índices estudiosos permitem a escolha de coleções de periódicos, aplicação de fundos de pesquisa, classificação de periódicos e determinação de contribuintes significativos em uma área de assunto.

Os advogados dos índices estudiosos recomendam seu uso em áreas como serviços de ligação, referências, instrução e gerenciamento de coleções.

Os críticos do uso de índices estudiosos citam suas limitações devido a questões de precisão, validade e aplicabilidade e debate sua aplicação à contratação, posse, financiamento, concessão de prêmios e decisões de associação.

Embora os índices estudiosos possam não descrever completamente o impacto do trabalho de um pesquisador individual, alguns acadêmicos determinarão seus próprios índices estudiosos a serem incluídos no material promocional e no currículo Vita, por exemplo. Outros podem estudar seus índices estudiosos simplesmente por si.

Os interessados ​​no campo dos índices estudiosos podem encontrar os resultados, por exemplo, projetos de visualização de dados, emocionantes.

Tipos

Até o momento, vários índices estudiosos foram desenvolvidos. Um é o 'H-Index', introduzido por Jorge E. Hirsch em agosto de 2005. Hirsch descreveu o índice H tão imparcial quanto envolveu a relação do volume de trabalhos publicados de um acadêmico e o número de citações para aqueles documentos que criavam menos viés do que ou medir sozinho.

Outro índice estudioso é o 'G-Index', que mede a contagem de citações de todas as obras bem citadas por um período de tempo. O 'm-quotient' foi desenvolvido para introduzir um limite de tempo para o índice H que era de outra forma, uma quantidade cada vez maior.

Outras variantes do índice H, como Hi-Index, E-Index e outras, estão sendo desenvolvidas e revisadas.

O número ERDőS foi desenvolvido para medir a cadeia de publicação iniciada por Paul Erdős.

Todos esses índices estudiosos quantificam a contribuição de um pesquisador com base apenas em citações de seu trabalho. Idealmente, uma avaliação da contribuição de um pesquisador para o seu campo incluiria os índices estudiosos e uma análise da qualidade do próprio trabalho.

INDEX H.

O índice H-Index foi sugerido por Jorge E. Hirsch, físico da UCSD, em 2005.

Henry Schaefer, da Universidade da Geórgia, EUA, juntamente com a colega Amy Peterson, criou rankings de acordo com o H-Index, da Web da Science ISI. Embora os aplicativos baseados na Web possam calcular os índices H, Peterson teve que verificar nomes incorretos ou duplicados.

O índice H é definido da seguinte forma:

A scientist has index h if h of his or her N papers have at least h citations each, and the other (N-h) papers have no more than h citations each.

Para calcular o índice H, os trabalhos escritos por um acadêmico são organizados em ordem decrescente de número de citações. O índice H é onde o número de trabalhos é igual ao número de citações (começando com o artigo com o maior número de citações).

Embora amplamente utilizado, o índice H não leva em consideração a qualidade dos papéis; outros trabalhos que citam as publicações acadêmicas; O número de co-autores e a posição do autor na lista de autores. Além disso, todos os campos recebem valor igual.

Outra limitação é que o índice H não varia com o tempo [citação necessária]. Por exemplo, Évariste Galois tinha um índice H de 2, enquanto Claude Shannon tinha um índice H de 7, aumentou para 62 em 2020.

m-quotient

Enquanto o índice H é independente da data da carreira de um acadêmico, o Quotiente M visa pesar o período de empreendimento acadêmico, para reduzir o viés em favor de cientistas com carreiras mais longas.

Assim, se n = número de anos desde o primeiro artigo publicado do cientista, o m-quotient = h-index/n.

No entanto, o Quotiente M pode não se estabilizar até mais tarde na carreira do cientista. Para os pesquisadores no início de sua carreira, com índices H baixos, pequenas mudanças no índice H podem levar a grandes mudanças no Quotiente M. Hirsch sugere que o primeiro artigo publicado do pesquisador nem sempre pode ser o ponto de partida apropriado, especialmente se foi uma pequena contribuição publicada bem antes do período de produtividade sustentada do acadêmico.

Embora o Quotiente M adicione tempo como fator de ponderação, ele não atende às principais desvantagens do índice H, incluindo a qualidade da publicação e a qualidade da citação.

G-Index

O G-Index é uma variante do índice H, que leva em consideração a evolução da citação dos artigos mais citados ao longo do tempo.

A set of papers has a g-index g if g is the highest rank such that the top g papers have, together, at least g^2 citations.

Em outras palavras, o Index G é a maior classificação (onde os documentos são organizados em ordem decrescente do número de citações que receberam), de modo que os primeiros documentos G tenham (juntos) pelo menos g^2 citações.

Pode-se provar que, para qualquer conjunto de trabalhos, sempre existe o Index G e é único.

g = (α -1 α -2) α -1 α 1 t α {\ displayStyle g = \ esquerda ({\ frac {\ alpha -1} {\ alpha -2}} \ direita)^{\ frac {\ alfa -1} {\ alpha}} {\ frac {1} {t^{\ alpha}}}}

onde o expoente lotkaian e onde t indica o número total de fontes.

Desde H = t 1 / α {\ displayStyle h = t^{1 / \ alpha}}, g = (α - 1 α - 2) α - 1 α h> h {\ displaystyle g = \ esquerda ({\ frac {\ alpha -1} {\ alpha -2}} \ right)^{\ frac {\ alpha -1} {\ alpha}} h> h}

Por exemplo, se 2 cientistas têm o H-Index 4, pode acontecer que um deles tenha publicado 4 trabalhos que tenham 4 ou mais citações, enquanto outro cientista pode ter publicado 10 artigos dos quais 3 têm mais de 100 citações e o 4º O artigo tem 4 citações e o restante tem menos de 4 citações.

Na tentativa de oferecer uma ponderação mais alta ao segundo cientista que, em agregação, recebeu mais de 304 citações por 10 artigos, o Index G foi proposto. Assim, em nosso exemplo, o primeiro cientista possui G-Index = 4, enquanto o segundo cientista tem um índice G significativamente maior.

Número Erdős

Um número ERDőS mede a distância colaborativa entre uma pessoa e o matemático Paul erdős, medido pela autoria de artigos matemáticos.

Considerando que Paul erdős tem um índice = 0, as pessoas que co-autoras com ele têm um índice = 1, co-autores desses co-autores têm índice = 2 e assim por diante. Assim, para calcular o número Erdős, adicione 1 ao número Erdős de qualquer co-autor com o número mais baixo de erddős. O projeto de número Erdős da Universidade de Oakland mantém um site que acompanha o número de cientistas em todo o mundo.

Uma advertência é que a maioria dos números ERDős registrados até agora varia de até 13, mas a média é menor que 5 e quase todo mundo com um número finito de ERDős tem um número menor que 8.

Hubs e índices de autoridade

A avaliação da contribuição completa de um estudioso para seu campo de pesquisa pode ser avaliada de duas maneiras. Uma é contabilizando o número de citações recebidas pelo estudioso. O outro é responsável pela qualidade das referências referidas pelo estudioso.

Enquanto ser fortemente citado faz de um estudioso uma forte autoridade em seu campo, ter referências fortes faz de um estudioso um centro forte, que conhece todo o trabalho significativo nesse campo. O cálculo dos índices de hub e autoridade requer o conhecimento das relações entre os estudiosos que estão sendo citados ou referidos.

O algoritmo de hubs e autoridades pode ser usado para calcular esses índices. O algoritmo realiza uma análise de link em uma determinada rede e atribui duas pontuações a cada nó: um hub e uma autoridade.;

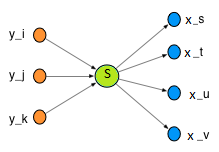
Um nó valioso e informativo em uma rede geralmente é apontado por um grande número de links, ou seja, possui um grande indegredo (ver Fig. 1). Esse nó é chamado de autoridade.

Um nó que aponta para muitos nós de autoridade é um recurso útil e é chamado de hub. Um hub geralmente possui um grande e ao ar livre. No contexto da citação da literatura, um hub é um artigo de revisão que cita muitos artigos originais, enquanto uma autoridade é um artigo seminal original que é citado por muitos artigos.

Uma rede pode ser construída de nós que representam autores e links indicando referências a artigos publicados. Os links de saída indicam quem o autor citou e os links recebidos indicam quem citou o autor.

A pontuação do centro de um pesquisador é a soma das pontuações dos autores cujo trabalho é citado. A pontuação da autoridade de um pesquisador é a soma das pontuações do hub dos autores que referenciaram o trabalho do pesquisador.

A pontuação do hub aumenta se o autor citar documentos publicados por autores com altas pontuações de autoridade. A pontuação da autoridade aumenta quando os artigos publicados são citados por autores com alta pontuação de hubs.

h (x) ← ∑ x → y a (y) {\ displayStyle h (x) \ leftarrow \ sum _ {x \ rightarrow y} a (y)}

a (x) ← ∑ y → x h (y) {\ displayStyle a (x) \ leftarrow \ sum _ {y \ rightarrow x} h (y)}

As equações podem ser reescritas em um formulário de vetor de matriz. Seja A uma matriz de adjacência da rede e vetores H e A para conter todos os hubs e pontuações das autoridades, respectivamente. Em seguida, as pontuações podem ser calculadas pelas seguintes fórmulas.

h → = (1 / λ h) a a t h → {\ displayStyle {\ vec {h}} = (1 / \ lambda _ {h}) aa^{t} {\ vec {h}}}}

a → = (1 / λ a) a a a → {\ displayStyle {\ vec {a}} = (1 / \ lambda _ {a}) a^{t} a {\ vec {a}}}

Implementação de algoritmo de hubs e autoridade

Os hubs e os índices das autoridades exigem o conhecimento da conectividade entre estudiosos que se referem e citam o trabalho um do outro. Como nem sempre é possível obter com precisão esses padrões de conectividade, a matriz de adjacência (a) em relação às conexões do estudioso pode ser estimada.

Por exemplo, um cientista possui uma matriz de conectividade local estimada. É uma combinação do trabalho pelo qual ele é citado e obras que ele cita. Depois que a rede de adjacência é estimada, os índices de hub e autoridade são determinados pela decomposição de auto-decomposição de (A.a ') e (a'.a), respectivamente. As etapas seguidas para esta implementação específica são as seguintes:

Step 1: Let the scholar to be evaluated be S. This scholar is searched in Scopus and the total number of citations he has received= c, and the total number of references he has used=r.Step 2: A list of scholars who have cited the works of S are recorded as a set Y. The list of scholars who have been referred by S are recorded as X. The choice of members of X and Y are made in the order of decreasing citations in Scopus. Since an estimate of adjacency matrix A was sufficient, thus, we recorded members of X, and Y with citations greater than 100 in Scopus. Let the number of significant citations = cs , and the number of significant references = rs . For each significant member of X and Y, one evaluates the ratio of (the number of citations/number of references) as weights of matrix A.Step 3: Once the weights corresponding to the significant members of X and Y are calculated, the weights of not-so-significant members are estimated randomly. Thus, random weights are generated for c − cs citations for members of Y and r − rs references for members of X. The matrix A is thus generated as:AColumnSXYRow indexS010X000Y100

Onde blocos de x e blocos de y substituem os '1's. A conectividade segue a Fig 2.

Step 4: The initial hub vector is calculated as primary eigen-vector (with the highest eigen-value) of A.A' and normalized between [0,1]. The initial authority vector is the primary eigen-vector of A'.A and normalized too. Since these indices are interrelated, thus, the hub vector becomes A*initial authority vector, and the authority vector becomes A'*initial hub vector. Since the scientist 'S' was the first entry of matrix A, hence the first value of the hub and authority vectors are the hub-authority indices for scientist S. The pseudocode for the same is as follows is S is a scholar whose hub index is h and authority index is a.

Pseudo-código

1 H I ← P R I N C I P A L E I G E N V E C T O R (A A T) {\ DisplayStyle H_ {I} \ LeAutrow Principal ~ Eigen ~ vetor (aa^{t})}

2 a i ← p r i n c i p a l e i g e n v e c t o r (a t a) {\ displayStyle a_ {i} \ leftarrow Principal ~ eigen ~ vetor (a^{t} a)}

3 h = a ∗ a i {\ displayStyle h = a*a_ {i}}

4 a = a t ∗ h i {\ displaystyle a = a^{t}*h_ {i}}

Exemplo 1: índices estudiosos de cientistas conhecidos

Scientisth-index (using Publish or Perish)g-index (using Publish or Perish)h-index (using Scopus)Hub index (per 10^2)Authority Index Newman, MEJ6521051210.54129.3687Einstein, Albert92231N/A (nothing submitted after 1995)099.9586Shannon, CE44228N/A (nothing submitted after 1995)015.9117Erdős, Paul7614280.40649077.8040Shenker, Scott1052533629.173171.1167Hirsch, Jorge E.31702178.938151.5361Pople, John8729329123.7993355.6553

A tabela utiliza apenas um mecanismo de pesquisa e a matriz de adjacência é uma estimativa, portanto, os resultados tabulados acima são versões extremamente agregadas e não devem ser confundidas com índices absolutos. Uma estimativa melhor da matriz de adjacência pode produzir variações nos índices. Além disso, o Scopus acompanha apenas os artigos após 1995, de modo que isso é uma restrição adicional. (Todos os índices foram avaliados em 12 de dezembro de 2011.)

Nesta tabela, é evidente que diferentes mecanismos de pesquisa produzem diferentes índices H. É possível que um cientista com alto índice H possa ser uma autoridade forte, mas não necessariamente um centro forte. A validade dos mecanismos de pesquisa na Web é avaliada como documentos antes de 1995, são inacessíveis. O número de publicações de um determinado autor em uma base de dados específica é responsável por afetar os índices de autoridade do hub. O trabalho interdisciplinar pode ser bem avaliado pelo Índice de Autoria Hub em oposição a outros índices.

Exemplo 2: índices projetados para autoridade de hub com tempo (exemplo de brinquedo)

Este é um exemplo para entender a interação dos vários índices estudiosos.

Uma nova cientista que iniciou sua carreira acadêmica em 2009 publicou 3 artigos. Dois trabalhos têm 2 citações cada, enquanto o terceiro artigo não tem citações. Ela referenciou 60 artigos com 17 referências fortes entre os 60. Um de seus co-autores tem o menor número 3. Seus índices estudiosos de dezembro de 2011 são:

h-index = 2g-index = 2m-quotient = 2/2=1Erdős number = 3+1=4HUB index (per 10^2) = 11.702AUTHORITY index = 0.1061

Em mais um ano, ela publica outro artigo com 20 novas referências, de modo que agora ela tem um cumulativo de 31 referências fortes, 4 artigos com 2 citações para 2 artigos e 0 citações para outros 2 artigos. Seus índices de autoridade de hub mudam:

Índice de cubo = 12.668

Índice de autoridade = 0,1061

Em mais um ano, suas citações para os 3 artigos aumentam para 10 e ela continua a ter 60 referências com 17 referências fortes:

Índice de hub = 11.568

Índice de autoridade = 0,3241

Em mais um ano, suas citações aumentam para 10 e ela escreve outro artigo de modo que o número de referências suba para 80 (com 31 fortes):

Índice de cubo = 12.694

Índice de autoridade = 0,3284

Assim, para resumir, os seguintes índices de autoridade do hub são observados para este exemplo de brinquedo.

InstanceNo. of citationsNo. of referencesHUB (per 10^2)AUTHORITYCurrently46011.7020.1061If references increase48012.6680.1061If citations increase106011.5680.3241If citations and references increase108012.6940.3284

O código MATLAB para as instâncias do Exemplo 1 e do Exemplo de Toy no Exemplo 2 é anexado como o arquivo 1.

Esses exemplos demonstram a importância dos índices de autoridade de hub na avaliação quantitativa das contribuições de um estudioso em uma carreira acadêmica completa.

Crítica

Os índices estudiosos têm limitações, incluindo falta de precisão, validade e aplicabilidade. Embora a precisão dos índices estudiosos seja questionável devido à diferença de grafias, diferença no analisador, mecanismos de pesquisa e bases de dados de documentos mantidas por várias fontes on -line, pode ser possível resolver os problemas de precisão se cada autor puder ser atribuído a um ID exclusivo Em vez de confiar nos nomes para pesquisas. Além disso, cada vez que esses índices são relatados, o método e os mecanismos de pesquisa utilizados devem ser mencionados para evitar a ambiguidade o máximo possível.

A validade dos índices estudiosos é uma limitação, porque eles não pesam campos de importância variável. Por exemplo, John Pople, um químico teórico que recebeu um prêmio Nobel, se sai mal em conjuntos de índices H.

A aplicabilidade dos índices estudiosos tem limitações quando os estudiosos enfatizam o avanço prático em uma área de empreendimento e não na publicação de artigos. Também é difícil documentar as obras de uma década anterior como documentos on -line, diminuindo assim seu fator de impacto on -line. Por exemplo, o Scopus é um banco de dados on -line que calcula os índices bolsistas para documentos encontrados apenas após 1995. Quaisquer trabalhos anteriores não estão documentados ou avaliados.

Jorge E. Hirsch sugeriu que o H-Index deveria informar comitês de contratação, promoção, financiamento, posse, prêmio e sociedade para tomar decisões criteriosas. No entanto, devido às suas limitações, elas são melhor vistas de maneira equilibrada.