Rede de gradiente
Content
Definição
O transporte ocorre em uma rede fixa g = g (v, e) {\ displayStyle g = g (v, e)} chamado de gráfico de substrato. Tem n nós, v = {0, 1 ,. . . , N-1} {\ displayStyle v = \ {0,1, ..., n-1 \}} e as bordas e = {(i, j) | i, j ∈ V} {\ displayStyle e = \ {(i, j) | i, j \ em v \}}. Dado um nó I, podemos definir seu conjunto de vizinhos em G por Si (1) = {j ∈ V | (i, j) ∈ E}.

Vamos também considerar um campo escalar, h = {h0, .., hn - 1} definido no conjunto de nós V, para que cada nó I tenha um valor escalar oi associado a ele.
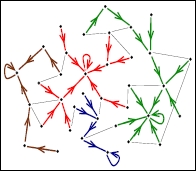
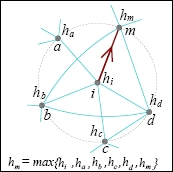
Gradiente ∇hi em uma rede: ∇hi = {\ displayStyle =} (i, μ (i)) isto é, isto é, a borda direcionada de i a μ (i), onde μ (i) ∈ Si (1) ∪ {i}, e Hμ tem o valor máximo em h j | j ∈ S i (1) ∪ i {\ displayStyle {h_ {j} | j \ em s_ {i}^{(1)} \ cup {i}}}.
Rede de gradiente: ∇ g = {\ displayStyle g =} ∇ g {\ displayStyle g} (v, f) {\ displayStyle (v, f)} onde f é o conjunto de bordas de gradiente em G.
Em geral, o campo escalar depende do tempo, devido ao fluxo, fontes externas e afundos na rede. Portanto, a rede de gradiente ∇ g {\ displaystyle g} será dinâmica.
Motivação e história
O conceito de rede de gradiente foi introduzido pela primeira vez por Toroczkai e Bassler (2004).
Geralmente, redes do mundo real (como gráficos de citação, Internet, redes metabólicas celulares, a rede aeroportuária mundial), que geralmente evoluem para transportar entidades como informações, carros, energia, água, forças e assim por diante, não são globalmente projetado; Em vez disso, eles evoluem e crescem através de mudanças locais. Por exemplo, se um roteador na Internet estiver frequentemente congestionado e os pacotes forem perdidos ou atrasados devido a isso, ele será substituído por vários novos roteadores interconectados.
Além disso, esse fluxo é frequentemente gerado ou influenciado pelos gradientes locais de um escalar. Por exemplo: A corrente elétrica é acionada por um gradiente de potencial elétrico. Nas redes de informações, as propriedades dos nós gerarão um viés na forma de informações são transmitidas de um nó para seus vizinhos. Essa idéia motivou a abordagem para estudar a eficiência de fluxo de uma rede usando redes de gradiente, quando o fluxo é acionado por gradientes de um campo escalar distribuído na rede.
Pesquisas recentes [qual?] [Precisa de atualização] investiga a conexão entre a topologia da rede e a eficiência do fluxo do transporte.
Distribuição em grau de redes de gradiente
Em uma rede de gradiente, o grau de um nó I, ki (in) é o número de bordas de gradiente apontando para i, e a distribuição em grau é r (l) = p {k i (i n) = l} { \ displayStyle r (l) = p \ {k_ {i}^{(in)} = l \}}.

Quando o substrato G é um gráfico aleatório e cada par de nós está conectado à probabilidade P (ou seja, um gráfico aleatório erdős -rényi), os escalares hi são i.i.d. (Independente distribuído idêntico) A expressão exata para r (l) é dada por
R ( l ) = 1 N ∑ n = 0 N − 1 C l N − 1 − n [ 1 − p ( 1 − p ) ] N − 1 − n − l [ p ( 1 − p ) n ] l ] {\displaystyle R(l)={\frac {1}{N}}\sum _{n=0}^{N-1}\mathrm {C} _{l}^{N-1-n}[1-p(1-p)]^{N-1-n-l}[p(1-p)^{n}]^{l}]}
No limite n → ∞ {\ displaystyle n \ to \ infty} e p → 0 {\ displayStyle p \ a 0}, a distribuição de grau se torna a lei de energia
R ( l ) ≈ l − 1 {\displaystyle R(l)\approx l^{-1}}
Isso mostra nesse limite, a rede de gradiente de rede aleatória é livre de escala.
Além disso, se a rede de substrato G estiver livre de escala, como no modelo Barabási-Albert, a rede de gradientes também seguirá o poder de energia com o mesmo expoente que o de G.
O congestionamento nas redes
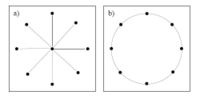
O fato de a topologia da rede de substrato influenciar o nível de congestionamento da rede pode ser ilustrado por um exemplo simples: se a rede tiver uma estrutura semelhante a estrela, então no nó central, o fluxo ficaria congestionado porque o nó central deve lidar todo o fluxo de outros nós. No entanto, se a rede tiver uma estrutura semelhante a um anel, pois cada nó assume o mesmo papel, não há congestionamento de fluxo.
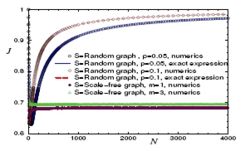
Sob suposição de que o fluxo é gerado por gradientes na rede, a eficiência do fluxo nas redes pode ser caracterizada através do fator intermediário (ou fator de congestionamento), definido da seguinte forma:
J = 1 − ⟨ ⟨ N receive N send ⟩ h ⟩ network = R ( 0 ) {\displaystyle J=1-\langle \langle {\frac {N_{\text{receive}}}{N_{\text{send}}}}\rangle _{h}\rangle _{\text{network}}=R(0)}
onde nreceive é o número de nós que recebem fluxo de gradiente e NSEND é o número de nós que enviam o fluxo de gradiente. O valor de j está entre 0 e 1; J = 0 {\ displayStyle j = 0} significa não congestão e j = 1 {\ displayStyle j = 1} corresponde ao congestionamento máximo.inn the limite n → ∞ {\ displayStyle n \ a \ infty}, para um erdős- Gráfico aleatório de Rényi, o fator de congestionamento se torna
J ( N , P ) = 1 − ln N N ln ( 1 1 − P ) [ 1 + O ( 1 N ) ] → 1. {\displaystyle J(N,P)=1-{\frac {\ln N}{N\ln({\frac {1}{1-P}})}}\left[1+O({\frac {1}{N}})\right]\rightarrow 1.}
Esse resultado mostra que as redes aleatórias estão no máximo congestionadas nesse limite. Em contrário, para uma rede sem escala, J é uma constante para qualquer n, o que significa que as redes sem escala não são propensas a intermaturas máximas.
Abordagens para controlar o congestionamento
Um problema nas redes de comunicação é entender como controlar o congestionamento e manter a função de rede normal e eficiente.
Zonghua Liu et al. (2006) mostraram que é mais provável que o congestionamento ocorra nos nós com altos graus nas redes, e uma abordagem eficiente de aprimorar seletivamente a capacidade de processo de mensagem de uma pequena fração (por exemplo, 3%) dos nós é demonstrado como executado bem também como melhorar a capacidade de todos os nós.
Pastore y Pionti et al. (2008) mostraram que a dinâmica relaxacional [esclarecimento necessária] pode reduzir o congestionamento da rede.
Pan et al. (2011) estudaram propriedades de interferência em um esquema em que as bordas recebem pesos de um poder da diferença escalar entre os potenciais dos nó. [Esclarecimento necessário]
NIU e Pan (2016) mostraram que o congestionamento pode ser reduzido pela introdução de uma correlação entre o campo de gradiente e a topologia da rede local. [Esclarecimento necessário]








