RELACIONAL DE RAMBERG - OSGOOD
Content
Comportamento de endurecimento e deslocamento de rendimento
Na última forma do modelo de Ramberg -OSGOOD, o comportamento de endurecimento do material depende das constantes do material α {\ DisplayStyle \ alpha \,} e n {\ displayStyle n \,}. Devido à relação da lei de potência entre estresse e tensão plástica, o modelo de Ramberg-OSGOOD implica que a tensão plástica está presente mesmo para níveis muito baixos de tensão. No entanto, para tensões baixas aplicadas e para os valores comumente usados das constantes do material α {\ displayStyle \ alpha} e n {\ displaystyle n}, a tensão plástica permanece insignificante em comparação com a tensão elástica. Por outro lado, para níveis de estresse mais altos que σ 0 {\ displayStyle \ sigma _ {0}}, a tensão plástica se torna progressivamente maior que a tensão elástica.
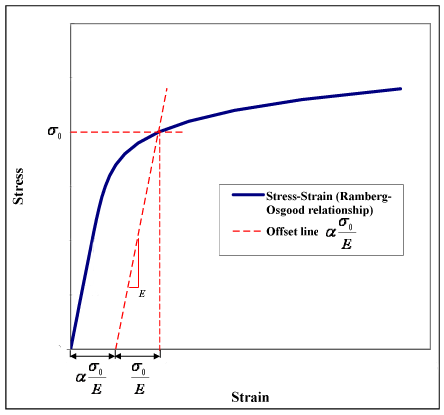
O valor α σ 0 e {\ displayStyle \ alpha {\ frac {\ sigma _ {0}} {e}}} pode ser visto como um deslocamento de rendimento, como mostra a Figura 1. Isso vem do fato de que ε = ( 1 + α) σ 0 / e {\ displayStyle \ varepsilon = (1+ \ alpha) {{\ sigma _ {0}} / {e}} \,}, quando σ = σ 0 {\ displaystyle \ sigma = \ Sigma _ {0} \,}.
Consequentemente, (veja a Figura 1):
elastic strain at yield = σ 0 / E {\displaystyle {{\sigma _{0}}/{E}}\,}
plastic strain at yield = α ( σ 0 / E ) {\displaystyle \alpha ({\sigma _{0}}/E)\,} 
= yield offsetOs valores comumente usados para n {\ displayStyle n \,} são ~ 5 ou mais, embora valores mais precisos sejam geralmente obtidos pelo ajuste de dados experimentais de tração (ou compressiva). Os valores para α {\ DisplayStyle \ alpha \,} também podem ser encontrados por meio de ajuste a dados experimentais, embora para alguns materiais possa ser fixado para ter o deslocamento igual ao valor aceito da tensão de 0,2%, que significa:
α σ 0 E = 0.002 {\displaystyle \alpha {\frac {\sigma _{0}}{E}}=0.002}
Formulações alternativas
Várias formulações alternativas ligeiramente diferentes da equação de Ramberg-Osgood podem ser encontradas. Como os modelos são puramente empíricos, geralmente é útil experimentar modelos diferentes e verificar que tem o melhor ajuste com o material escolhido.
A equação de Ramberg-Osgood também pode ser expressa usando os parâmetros Hollomon em que K {\ DisplayStyle K} é o coeficiente de força (PA) e N {\ displayStyle n} é o coeficiente de endurecimento da tensão (sem unidades).
ε = σ e + (σ k) 1 / n {\ displayStyle \ varepsilon = {\ frac {\ sigma} {e}} + \ esquerda ({\ frac {\ sigma} {k}} \ direita)^{1 1 /n}}
Alternativamente, se a tensão de escoamento, σ y {\ displaystyle \ sigma _ {y}}, é assumida como na tensão de deslocamento de 0,2%, o seguinte relacionamento pode ser derivado.
ε = σ e + 0,002 (σ σ y) n {\ displayStyle \ varepsilon = {\ frac {\ sigma} {e}} + 0,002 \ esquerda ({\ frac {\ sigma} {\ sigma _ {}}} \ direita)^{n}}